(1)のつづき。
さて、ダイヤをおこがましくも評価すると書いてみたが、どういう観点で評価すればいいだろうか。既存の研究※では、乗客はそれぞれの「コスト(不効用)」が最も小さくなるように行動するというモデルが提唱されている。具体的には、A駅からB駅への「コスト」は、所要時間・乗り換え回数・混雑率をそれぞれ仮想的な時間に変換して和をとる方法で計算されている。
※利用者均衡配分法による通勤列車運行計画の利用者便益評価, 家田仁・赤松隆・高木淳・畠中秀人,土木計画学研究論文集 No.6, '88年11月, pp.177-184 あたりが有名だろう
このモデルは、混雑率が高かったり、あまりにも乗り換えが不便や回数の多いルートについては、少々所要時間が短くても選択されない可能性について指摘している。ただし、ここでは混雑率を指標に入れることは、実際の観察etc.が必要で困難なことや、京急は快特集中主義に現状なっており、普通と優等の速度差が激しいため、追い抜かれる普通を乗り通す客の総数は少ないと見なし、コストとして「所要時間」を評価の対象とすることとする。
※横浜~上大岡のように、南太田で退避する普通(後続の快特が早く着く場合)にあえて乗る場合もあるだろうが、ここでは有効列車に含めないこととする
ここで書いた「所要時間」とは、A駅に到着してから目的のB駅で降りるまでの乗車時間・待ち時間・乗り換え時間を全て含めたものとする。ここで問題になるのがA駅(出発駅)に到着してから、目的の電車に乗るまでの待ち時間をどうカウントするかだが、出発駅に到着する乗客は一様分布する(ランダムに到着する)ものとする。
到着モデルについても先ほどの論文やその他の乗客流動やダイヤ評価関連の論文でも言及されているが、乗り換えに特化し、なおかつ特定の時刻にスポット的に大量の乗客が現れるような駅は京急線内では考えづらく、巨視的に見ればこのモデルを採用しても特に問題ないと考えられる。
横浜や品川といった乗り換え客が多数いる駅は、京急に乗り換える元の電車の候補がたくさんあり、その駅からの乗客も多いため、ならせば均一に乗客が現れると見なしても差し支えないだろう。
※泉岳寺は直通客が多くを占めると考えられるが、泉岳寺以遠からの乗客を仮想的に一駅にまとめ、特別扱いすることで問題ないと思われる。今回はそこの計算は特にしておらず、各駅から純粋に改札を通って乗車する乗客を対象としている。
また、乗客は駅に到着した時点で最速の乗り継ぎ(ただし京急線内に限定)ルートで目的駅に到着するものとし、折り返し乗車は認めない(品川→蒲田→梅屋敷のような折り返しはたとえ最速でも考慮しない)ものとする。Webサービスの乗換案内で検索したときに最速のルートとして提示されたものを選んで乗車するような感じになる。
なお、これを考えると、各駅に何分に来たときの最速パターンというのを計算する必要がある。たとえば、品川から羽田空港の間は、12:02~12:07の間に来たら07分発のエア急で、12:07~16の間は16分発のエア快特、12:16~22の間は22分発のSH快特に乗って蒲田で乗り換えが最速というように。
これはグラフ理論(ノード/リンク構造)でダイヤグラムを表現して最短経路探索をすることで計算可能となるが、本筋でないので省略する。
なお、ダイヤの情報としては「えきから時刻表」「東京時刻表」を用いる。業務用のダイヤグラムでないため分単位に丸められているかげ、±30秒の誤差があると考えれば、所要時間の誤差は発車駅・到着駅を合わせて最大で1分になる。
以上より、たとえば品川から羽田空港に当てはめると、
・12:02のSH快特→乗車所要時間20分(蒲田乗換え)
・12:07のエア急→乗車所要時間22分
・12:16のエア快→乗車所要時間17分
・12:22のSH快特→乗車所要時間20分(蒲田乗換え)
:
の20分サイクルが繰り返す構造となっている。京急は平日日中と、土休日は早朝深夜を除き同じサイクルが繰り返すため、この繰り返しが続くと見なして所要時間が計算できる。
このとき、品川駅への乗客の到着時間tと、その時間に到着したときの羽田空港までの所要時間をf(t)とすると、以下の図に示すような関係になる。
#すんげーきたないグラフですがご容赦ください。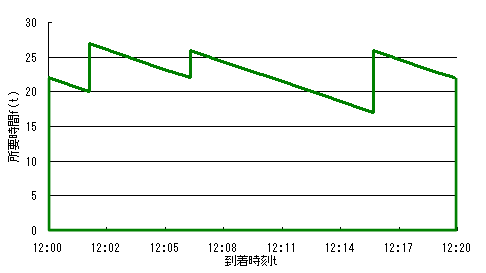
先ほど、出発駅の乗客は一様分布に到着すると仮定したため、平均所要時間は∫f(t)dt / 20と計算できる。いきなり積分記号が出てきたが、そんなに難しいことではなく、上のグラフを同一面積のまま横幅20の長方形にしたとき(下図の赤い四角形)の縦軸の長さを求めていることに等しい。その縦軸の長さが平均所要時間となる。この場合は平均所要時間は22.7分となる。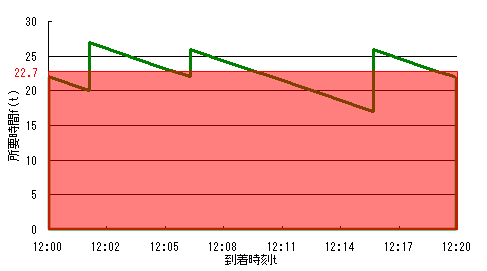
さて、これらの条件をもとに、各駅間の平均所要時間を計算してみることにする。
(続く)
さて、ダイヤをおこがましくも評価すると書いてみたが、どういう観点で評価すればいいだろうか。既存の研究※では、乗客はそれぞれの「コスト(不効用)」が最も小さくなるように行動するというモデルが提唱されている。具体的には、A駅からB駅への「コスト」は、所要時間・乗り換え回数・混雑率をそれぞれ仮想的な時間に変換して和をとる方法で計算されている。
※利用者均衡配分法による通勤列車運行計画の利用者便益評価, 家田仁・赤松隆・高木淳・畠中秀人,土木計画学研究論文集 No.6, '88年11月, pp.177-184 あたりが有名だろう
このモデルは、混雑率が高かったり、あまりにも乗り換えが不便や回数の多いルートについては、少々所要時間が短くても選択されない可能性について指摘している。ただし、ここでは混雑率を指標に入れることは、実際の観察etc.が必要で困難なことや、京急は快特集中主義に現状なっており、普通と優等の速度差が激しいため、追い抜かれる普通を乗り通す客の総数は少ないと見なし、コストとして「所要時間」を評価の対象とすることとする。
※横浜~上大岡のように、南太田で退避する普通(後続の快特が早く着く場合)にあえて乗る場合もあるだろうが、ここでは有効列車に含めないこととする
ここで書いた「所要時間」とは、A駅に到着してから目的のB駅で降りるまでの乗車時間・待ち時間・乗り換え時間を全て含めたものとする。ここで問題になるのがA駅(出発駅)に到着してから、目的の電車に乗るまでの待ち時間をどうカウントするかだが、出発駅に到着する乗客は一様分布する(ランダムに到着する)ものとする。
到着モデルについても先ほどの論文やその他の乗客流動やダイヤ評価関連の論文でも言及されているが、乗り換えに特化し、なおかつ特定の時刻にスポット的に大量の乗客が現れるような駅は京急線内では考えづらく、巨視的に見ればこのモデルを採用しても特に問題ないと考えられる。
横浜や品川といった乗り換え客が多数いる駅は、京急に乗り換える元の電車の候補がたくさんあり、その駅からの乗客も多いため、ならせば均一に乗客が現れると見なしても差し支えないだろう。
※泉岳寺は直通客が多くを占めると考えられるが、泉岳寺以遠からの乗客を仮想的に一駅にまとめ、特別扱いすることで問題ないと思われる。今回はそこの計算は特にしておらず、各駅から純粋に改札を通って乗車する乗客を対象としている。
また、乗客は駅に到着した時点で最速の乗り継ぎ(ただし京急線内に限定)ルートで目的駅に到着するものとし、折り返し乗車は認めない(品川→蒲田→梅屋敷のような折り返しはたとえ最速でも考慮しない)ものとする。Webサービスの乗換案内で検索したときに最速のルートとして提示されたものを選んで乗車するような感じになる。
なお、これを考えると、各駅に何分に来たときの最速パターンというのを計算する必要がある。たとえば、品川から羽田空港の間は、12:02~12:07の間に来たら07分発のエア急で、12:07~16の間は16分発のエア快特、12:16~22の間は22分発のSH快特に乗って蒲田で乗り換えが最速というように。
これはグラフ理論(ノード/リンク構造)でダイヤグラムを表現して最短経路探索をすることで計算可能となるが、本筋でないので省略する。
なお、ダイヤの情報としては「えきから時刻表」「東京時刻表」を用いる。業務用のダイヤグラムでないため分単位に丸められているかげ、±30秒の誤差があると考えれば、所要時間の誤差は発車駅・到着駅を合わせて最大で1分になる。
以上より、たとえば品川から羽田空港に当てはめると、
・12:02のSH快特→乗車所要時間20分(蒲田乗換え)
・12:07のエア急→乗車所要時間22分
・12:16のエア快→乗車所要時間17分
・12:22のSH快特→乗車所要時間20分(蒲田乗換え)
:
の20分サイクルが繰り返す構造となっている。京急は平日日中と、土休日は早朝深夜を除き同じサイクルが繰り返すため、この繰り返しが続くと見なして所要時間が計算できる。
このとき、品川駅への乗客の到着時間tと、その時間に到着したときの羽田空港までの所要時間をf(t)とすると、以下の図に示すような関係になる。
#すんげーきたないグラフですがご容赦ください。

先ほど、出発駅の乗客は一様分布に到着すると仮定したため、平均所要時間は∫f(t)dt / 20と計算できる。いきなり積分記号が出てきたが、そんなに難しいことではなく、上のグラフを同一面積のまま横幅20の長方形にしたとき(下図の赤い四角形)の縦軸の長さを求めていることに等しい。その縦軸の長さが平均所要時間となる。この場合は平均所要時間は22.7分となる。

さて、これらの条件をもとに、各駅間の平均所要時間を計算してみることにする。
(続く)

コメントする